sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

setembro 22, 2021

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

setembro 20, 2021

 sistema indeterminístico Graceli ;

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

 SISTEMA GRACELI INFINITO-DIMENSIONAL.

COM  ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.

ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.

  TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA.

SISTEMA MULTIDIMENSIONAL  GRACELI

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].

DENTRO DE UMA CONCEPÇÃO QUE CADA ÁTOMO É FORMADO DE INFINITAs OUTRAS PARTÍCULAS, E COM INFINITAS OUTRAS ENERGIAS, INTERAÇÕES, TRANSFORMAÇÕES, E OUTROS FENÔMENOS, LOGO SE TEM EM CADA ÁTOMO E OU ELEMENTO QUÍMICO INFINITAS OUTRAS DIMENSÕES. COM INFINITAS VARIAÇÕES NAS CATEGORIAS DE GRACELI , QUE  SÃO: OS POTENCIAIS, TIPOS, NÍVEIS, E TEMPO DE AÇÃO ESPECÍFICO  DO FENÔMENO.

ONDE NOS SISTEMAS  DE GRACELI CATEGORIAS,  FENÔMENOS, ESTADOS, ENERGIAS, ESTRUTURAS, E OUTROS SÃO TIPOS E FORMAS DE DIMENSÕES..

FLUXOS ALEATÓRIOS DE ENERGIAS ELÉTRICA,  E FLUXOS DE SALTOS QUÂNTICOS INFINITESIMAIS E INDETERMINADOS.

SENDO QUE VARIAM CONFORME O SISTEMA INFINITO-DIMENSIONAL GRACELI.

A massa de Planck é a unidade de massa, notada por m_P, no sistema de unidades naturais conhecido por unidades de Planck. Nomeadas em homenagem a Max Planck, é a massa para a qual o raio de Schwarzschild é igual ao comprimento Compton dividido por π.

O valor da massa de Planck ${\displaystyle (M_{p})}$ se expressa por uma fórmula que combina três constantes fundamentais, a constante de Planck (h), a velocidade da luz (c) e a constante de gravitação universal (G):

${\displaystyle m_{P}={\sqrt {\frac {\hbar c}{G}}}}$ ≈ 1,2209 × 10¹⁹ GeV/c² = 2,176 × 10^-8 kg^[1]

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

sendo ${\displaystyle \hbar ={\frac {h}{2\pi }}}$ a constante reduzida de Planck.

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A CODATA 2002 - recomendou que o valor para a massa de Planck é 2,176 45(16) × 10⁻⁸ kg, aonde a parte entre parênteses indica a incerteza nos últimos dígitos mostrados — que é, um valor de 2,17645 × 10⁻⁸ kg ± 0,00016 × 10⁻⁸ kg.

Físicos de partículas e cosmólogos frequentemente usam a massa Planck reduzida, a qual é

${\displaystyle {\sqrt {\frac {\hbar {}c}{8\pi G}}}}$ ≈ 4,340 µg.

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Adicionando o 8π simplifica várias equações em gravidade.

Diferentemente da maioria das outras unidades de Planck, a massa de Planck está em uma escala mais ou menos concebível a humanos, como a massa corporal de uma pulga é aproximadamente 4000 a 5000 m_P.

Índice

• 1Significância
• 2Referências
• 3Ver também
• 4Bibliografia
• 5Ligações externas

Significância

A massa de Planck é a massa de um buraco negro no qual o raio de Schwarzschild multiplicado por π iguala seu comprimento de onda de Compton. Isto pode ser pensado como da massa em que uma partícula tem a mesma energia (${\displaystyle E=mc^{2}}$) 

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

que um fóton de comprimento de onda λ ${\displaystyle ({\mbox{E}}\ ={\frac {hc}{\lambda }}),}$ 

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde λ dividido por π é também o raio no qual a velocidade de escape torna-se maior que a velocidade da luz ${\displaystyle ({\frac {\lambda }{\pi }}={\frac {2Gm}{c^{2}}})}$,

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

 causando na partícula o colapso contínuo sobre si própria. Em outras palavras, é o raio do qual um buraco negro é aproximadamente o comprimento de Planck, o qual acredita-se ser a escala de comprimento na qual tanto a relatividade quanto a mecânica quântica simultaneamente tornam-se importantes.

Em outros termos, a massa de Planck é a quantidade de massa que, incluida em uma esfera cujo raio fosse igual ao comprimento de Planck, geraria uma densidade da ordem de 10⁹³ g/cm³. Segundo a física atual, esta teria sido a densidade do Universo após um intervalo de tempo da ordem de ${\displaystyle {10}^{-43}}$ segundos depois do Big Bang, o chamado tempo de Planck.

Em física, o tempo de Planck, (t_P), é a unidade de tempo no sistema de unidades naturais, conhecidas como unidades de Planck. Neste intervalo de tempo a luz viaja, no vácuo, uma distância que define a unidade natural conhecida por comprimento de Planck.^[1] A unidade recebe esse nome em referência a Max Planck, o primeiro a propô-la.

O tempo de Planck é definido como:

${\displaystyle t_{P}={\sqrt {\frac {\hbar G}{c^{5}}}}\approx 5.391247(60)\times 10^{-44}{\mbox{ s}}}$^[2]

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde:

${\displaystyle \hbar =h/2\pi }$ é a constante de Planck reduzida

G = constante gravitacional

c = velocidade da luz no vácuo

s é a unidade de tempo do sistema internacional, o segundo.

Os dois dígitos entre parênteses denotam o erro padrão do valor estimado.

Tempo de Planck é o tempo passado sobre o Big Bang a partir do qual as implicações da teoria da relatividade geral passaram a ser válidas. Este intervalo de tempo situa-se na ordem dos 10⁻⁴³ s. Para regressões menores que o tempo de Planck é necessária uma teoria quântica da gravidade para explicar os fenômenos observados. Embora separado do instante inicial por uma fração ínfima de segundo, o Tempo de Planck não se confunde com o momento do Big Bang, porque a matéria energia passou por mudanças dramáticas naqueles pedaços infinitesimais de tempo que se sucedera a ocorrência da explosão inicial, que permitiu a expansão das 3 dimensões espaciais a que estamos acostumados a viver (altura x largura x profundidade) ao longo da 'linha do tempo'.

Para ajudar a comparar diferentes ordens de magnitude, a seguinte lista descreve vários níveis de massa entre 10⁻³⁶ kg e 10⁵³ kg.

Fator (kg)	Valor	Item
10−36	1.783×10−36 kg	Um eV/c², a massa equivalente de um eletronvolt de energia.
	3.6×10−36 kg	Elétron neutrino, limite superior de massa (2 eV/c²)
10−35
10−34
10−33
10−32
10−31	9.11×10−31 kg	Elétron (511 MeV/c²), a mais leve partícula elementar com uma massa de repouso não nula.
10−30
10−29
10−28	1.9×10−28 kg	Múon (106 MeV/c²)
10−27 yoctograma (yg)	1.661×10−27 kg	Unidade de massa atômica (u) ou dalton (Da)
	1.673×10−27 kg	Próton (938.3 MeV/c²)
	1.674×10−27 kg	Átomo de hidrogênio, o mais leve átomo
	1.675×10−27 kg	Nêutron (939.6 MeV/c²)
10−26	1.15×10−26 kg	Átomo de lítio (6.941 u)
	2.99×10−26 kg	Molécula de água (18.015 u)
	7.95×10−26 kg	Átomo de titânio (47.867 u)
10−25	1.79×10−25 kg	Átomo de prata (107.8682 u)
	1.6×10−25 kg	bóson Z (91.2 GeV/c²)
	3.1×10−25 kg	Quark "top" (173 GeV/c²), a mais pesada partícula elementar conhecida
	3.2×10−25 kg	Molécula de cafeína (194 u)
	3.45×10−25 kg	Átomo de chumbo-208, o mais pesado isótopo estável conhecido
10−24 zeptograma (zg)
10−23
10−22	1.1×10−22 kg	Molécula de hemoglobina A do sangue
10−21 attograma (ag)
10−20	10−20 kg	Um pequeno vírus
10−19
10−18 femtograma (fg)
10−17	1.1×10−17 kg	Massa equivalente de um joule
	4.6×10−17 kg	Massa equivalente de uma caloria
10−16	7×10−16 kg	Bactéria Escherichia coli (E. coli)
10−15 picograma (pg)
10−14
10−13
10−12 nanograma (ng)	10−12 kg	Célula humana média (1 nanograma)
10−11
10−10	3.5×10−10 kg	Um pequeno grão de areia (0,063 mm de diâmetro, 350 nanogramas)
10−9 micrograma (µg)	2×10−9 kg	Massa do óvulo humano, na massa incerta do quilograma protótipo (2 microgramas)
10−8	2.2×10−8 kg	Massa de Planck
10−7
10−6 miligrama (mg)	1–2×10−6 kg	Massa típica de um mosquito (1–2 miligramas)
10−5 centigrama (cg)	1.1×10−5 kg	Grão grande de areia (2 mm de diâmetro, 11 miligramas)
10−4 decigrama (dg)	1.5×10−4 kg	Quantidade típica de cafeína em uma xícara de café (150 miligramas)
	2×10−4 kg	Carat métrica (200 miligramas)
10−3 grama (g)	10−3 kg	Um centímetro cúbico de água (1 grama)
	8×10−3 kg	Moedas típicas: euro (7.5 gramas) e Dólar dos E.U. A. (8.1 gramas)
10−2 decagrama (dag)	1.2–4×10−2 kg	Camundongo adulto (Mus musculus, 12–40 gramas)
	2.4×10−2 kg	Quantidade de etanol em uma dose de destilado (24 gramas)
	2.8×10−2 kg	Onça (avoirdupois) (28.35 gramas)
10−1 hectograma   (hg)	0.15 kg	Fígado humano (150 gramas)
	0.454 kg

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

1 kg e mais

Fator (kg)	Valor	Item
1 kg quilograma (kg)	1 kg	Um litro de água, aprox.
	3 kg	Bebê humano recém-nascido
	4.0 kg	Women's shotput
	5–7 kg	Gato doméstico
	7.26 kg	Men's shotput
101 miriagrama (mag)	10–30 kg	Um monitor CRT de computador, ou uma televisão CRT.
	15–20 kg	Cão de tamanho médio
	70 kg	Humano adulto; cão grande
102 quintal métrico (q)	180–250 kg	Leão maduro, fêmea (180 kg) e macho (250 kg)
	700 kg	Vaca
	907.18474 kg	1 tonelada curta (2000 libras - EUA)
103 megagrama (Mg) (ou tonelada métrica) (t)	1000 kg	Tonelada métrica/ton; um metro cúbico de água
	1016.0469088 kg	Ton (Britânica) / 1 tonelada longa (2240 libras - EUA)
	800–1600 kg	Automóvel de passeio típico
	3000–7000 kg	Elefante adulto
	5000 kg	Uma colher de chá (5 ml) de material das anãs brancas (5 tons)
104	1.1×104 kg	Telescópio espacial Hubble (11 tons)
	1.2×104 kg	O maior elefante registrado (12 tons)
	1.4×104 kg	Sino do Big Ben (14 tons)
	4.4×104 kg	Carga normal de um caminhão cavalo mecânico-reboque (44 tons)
	6.0×104 kg	O maior meteorito, Meteorito Hoba West (60 tons)
	8–10×104 kg	Maior dinossauro conhecido, o Argentinosaurus (80–100 tons)
105	1.8x105 kg	O maior animal conhecido, a baleia azul (180 tons)
	1.87×105 kg	Estação Espacial Internacional (187 tons)
	6×105 kg	Antonov An-225 (o mais pesado avião) com carga máxima (600 tons); vazio: 250 tons
106 gigagrama (Gg)	1.25×106 kg	Tronco da Sequóia gigante chamada General Sherman (1250 tons)
	1.5×106 kg	Portão individual da Barreira do Tâmisa
	2.041×106 kg	Massa no lançamento do Space Shuttle (2041 tons)

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Ligações externas

Em física, comprimento de Planck, denotado por ℓ_P, é uma unidade de comprimento igual a 1,616199(97) × 10⁻³⁵ m e corresponde à distância que a luz percorre no vácuo durante um tempo de Planck. É unidade básica do Sistema de Unidades de Planck.

O comprimento de Planck pode ser definido a partir de três constantes físicas fundamentais, quais sejam: a velocidade da luz no vácuo c, a constante de Planck e a constante gravitacional.

O comprimento de Planck desempenha uma função importante na física moderna, pois para comprimentos inferiores a este, tanto a mecanica quântica, como a relatividade geral deixam de conseguir descrever os comportamentos de particulas. Espaços inferiores ao comprimento de Planck têm sido alvo de exaustiva investigação na busca de uma teoria unificadora da relatividade com a mecânica quântica.

Valor

O comprimento de Planck ℓ_P é definido como

${\displaystyle \ell _{\mathrm {P} }={\sqrt {\frac {\hbar G}{c^{3}}}}\approx 1.616\;229(38)\times 10^{-35}\ \mathrm {m} }$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ${\displaystyle c}$ é a velocidade da luz no vácuo, G é a constante gravitacional e ħ é a constante de Planck reduzida.^[1][2]

O comprimento de Planck é aproximadamente 10⁻²⁰ vezes o diâmetro de um próton.

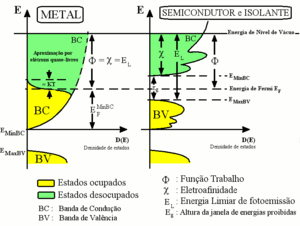
A Energia de Fermi é a energia do nível ocupado mais energético em um sistema quântico fermiônico à temperatura de zero absoluto. A definição estende-se também a sistemas acima do zero absoluto, caso em que a energia de fermi corresponde à energia obtida mediante uma média das energias dos níveis quânticos com probabilidade de ocupação - devido à agitação térmica - diferentes da unidade, cada qual ponderado pela respectiva probabilidade de ocupação. Associa-se via de regra à energia de fermi a notação E_F, e a nomenclatura retrata nítida homenagem ao físico ítalo-americano Enrico Fermi.

Índice

• 7Ver também

Introdução

Contexto geral

A energia de Fermi é importante na hora de entender o comportamento de partículas fermiônicas, como por exemplo os elétrons. Os férmions são partículas de spin semi-inteiro para as quais verifica-se a validade do princípio de exclusão de Pauli - que dita que dois férmions idênticos não podem ocupar simultaneamente o mesmo estado quântico. Desta maneira, quando um sistema possui vários elétrons, estes ocuparão níveis de energia maiores a medida que os níveis inferiores estejam preenchidos.

A energia de Fermi é um conceito que tem muitas aplicações na teoria dos orbitais atômicos, no comportamento dos semicondutores e na física do estado sólido em geral.

Em física do estado sólido a superficie de Fermi é a superficie no espaço de momentos na qual a energia de excitação total se iguala à energia de Fermi. Esta superfície pode ter uma topologia não trivial. Simplificadamente se pode dizer que a superfície de Fermi divide os estados electrônicos ocupados dos que permanecem livres.

Enrico Fermi e Paul Dirac, derivaram as estatísticas de Fermi-Dirac. Estas estatísticas permitem predizer o comportamento de sistemas formados por um grande número de elétrons, especialmente em corpos sólidos.

A energia de Fermi de um gás de Fermi (ou gás de elétrons livres) não relativista tridimensional se pode relacionar com o potencial químico através da equação:

${\displaystyle \mu =\epsilon _{F}\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {kT}{\epsilon _{F}}}\right)^{2}+{\frac {\pi ^{4}}{80}}\left({\frac {kT}{\epsilon _{F}}}\right)^{4}+...\right]}$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde ε_F é a energia de Fermi, k é a constante de Boltzmann e T é a temperatura. Portanto, o potencial químico é aproximadamente igual a a energia de Fermi à temperaturas muito inferiores a uma energia característica denominada Temperatura de Fermi, ε_F/k. Esta temperatura característica é da ordem de 10⁵K para um metal a uma temperatura ambiente de (300 K), pelo que a energia de Fermi e o potencial químico são essencialmente equivalentes. Este é um detalhe significativo dado que o potencial químico, e não a energia de Fermi, é quem aparece nas estatísticas de Fermi-Dirac.

Contexto avançado

Principais energias em estrutura de bandas para sólidos cristalinos.

Elétrons são férmions, ou seja, são partículas regidas pela estatística de Fermi. Nesta estatística, um dado estado quântico pode ser ocupado por no máximo um e não mais que um férmion, e portanto a máxima probabilidade de ocupação de um dado estado quântico é um. Os elétrons situados dentro da amostra estão confinados por um potencial atrativo exercido pelos íons positivos da rede. Conforme mostrado pela mecânica quântica, potenciais confinantes apresentam níveis de energias discretos. No caso dos átomos isto se reflete nos tão conhecidos níveis atômicos de energia e no caso dos sólidos cristalinos, a aproximação entre os átomos leva a um agrupamento dos estados em bandas de energia. Estas bandas são vistas nas relações de dispersão para os sólidos como sendo as regiões de energia permitidas para os elétrons, separadas umas das outras por janelas de energias proibidas (ou “gaps”).

Rigorosamente falando,^[1] a energia do nível de Fermi é definida em sistemas à temperatura de zero absoluto. Nesse caso, a energia do nível de Fermi é a energia do nível mais energético ocupado, visto que nessa temperatura todos os níveis com energia menor que a energia do nível de Fermi estariam ocupados (probabilidade igual a 1) e todos os níveis com energia acima, desocupados (probabilidade de ocupação nula). Para sistemas em temperaturas não nulas, não temos mais uma transição abrupta da probabilidade de ocupação, e sim uma probabilidade dada pela distribuição de Fermi-Dirac. Considera-se então como a energia do nível de Fermi a energia obtida pela média aritmética ponderada das energias de cada estado energético afetado pela excitação térmica (estados com probabilidades de ocupação diferentes de 1 ou 0) pesadas cada qual pela respectiva probabilidade de ocupação do estado associado. O denominador desta média será obviamente o número de estados envolvidos no processo. Repare que em acordo com a estatística de Fermi, dentre os referidos estados os menos energéticos têm probabilidade de ocupação maior do que aqueles mais energéticos. Para aproximação de elétrons livres a densidade de estados cresce com a raiz quadrada da energia, resultando em uma parábola no gráfico de energia x densidade de estados. Em semicondutores e isolantes esta dependência pode ser bem mais complicada.

Outra definição equivalente implica dizer que a energia de Fermi corresponde ao potencial eletroquímico do sistema na temperatura de zero absoluto. Uma extensão a temperaturas maiores é evidente, e a energia de Fermi corresponde assim ao potencial eletroquímico do sistema na temperatura considerada. A energia de Fermi expressa, portanto, qual seria a variação da energia interna total do sólido, considerado sempre como sistema isolado e em equilíbrio termodinâmico, caso um elétron fosse dele removido. Sendo E_N^total a energia total do sistema no estado neutro, em seu equilíbrio termodinâmico, e E_N-1^total a energia total do sistema também em seu novo equilíbrio termodinâmico mas após a remoção do elétron, temos que:

E_F = E_N^total - E_N-1^total

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Nas definições acima, o nível de referência é o nível de menor energia disponível aos N elétrons, e a remoção de um elétron provoca, então, a redução da energia do sistema. Neste referencial a energia de Fermi é, portanto, positiva, bem como o potencial eletroquímico.

Quando dois materiais diferentes são colocados em contato, a condição de equilíbrio termodinâmico exige que as suas energias de Fermi sejam iguais. Se as energias de Fermi fossem diferentes, a passagem de um elétron do sólido com maior energia de Fermi para o sólido com menor energia de Fermi resultaria em uma diminuição da energia total do sistema e o sistema composto não estaria, então, em sua configuração de equilíbrio, a de mínima energia, conforme exigido pelas leis da termodinâmica. Este fato dá origem a um fenômeno conhecido por diferença de potencial de contato que encontra diversas aplicações práticas, a saber na eletrônica de estado sólido (junção PN) e no uso do metal de sacrifício em navios.

Ilustração do conceito para compartimento monodimensional quadrado

A monodimensional compartimento quadrado infinito é um modelo para uma caixa mono dimensional. É um sitema modelo padrão em mecânica quântica para o qual a solução para uma partícula isolada é bem conhecido. Os níveis são marcados por um único número quântico n e as energias são dadas por

${\displaystyle E_{n}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n^{2}\,}$.

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Suponha-se agora que em vez de uma partícula nesta caixa nós temos N partículas na caixa e que estas partículas são férmions com spin 1/2. Então somente duas partículas podem ter a mesma energia i.e. duas partículas podem ter a energia de ${\displaystyle E_{1}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}}$, 

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

ou duas partículas podem ter energia ${\displaystyle E_{2}=4E_{1}}$ e assim por diante. A razão que duas partículas podem ter a mesma energia é que uma partícula de spin 1/2 pode ter um spin de 1/2 (spin "acima") ou um spin de -1/2 (spin "abaixo"), conduzindo a dois estadois para cada nível de energia. Quando nós olhamos na energia total deste sistema, a configuração para as quais a energia total é a menor (o estado fundamental), é a configuração onde todos os níveis de energia acima de n=N/2 estão ocupados e todos os níveis mais altos estão vazios. A energia de Fermi é consequentemente

${\displaystyle E_{f}=E_{N/2}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}(N/2)^{2}\,}$.

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O caso tridimensional

O caso tridimensional isotrópico é conhecido como a esfera de Fermi.

Deixe-nos agora considerar uma caixa cúbica tridimensional que tem um lado de comprimento L (ver compartimento quadrado infinito). Este torna-se uma muito boa aproximação para descrever elétrons em um metal.

Os estados agora são marcados po três números quânticos n_x, n_y, e n_z. As energias da partícula isolada são

${\displaystyle E_{n_{x},n_{y},n_{z}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}\right)\,}$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

n_x, n_y, n_z são inteiros positivos.

Existem múltiplos estados com a mesma energia, por exemplo ${\displaystyle E_{100}=E_{010}=E_{001}}$. Agora deixemos colocar-se N férmions não interativos de spin 1/2 nesta caixa. Para calcular a energia de Fermi, nós veremos no caso de que N é grande.

Se nós introduzios um vetor ${\displaystyle {\vec {n}}=\{n_{x},n_{y},n_{z}\}}$ então cada estado quântico corresponde a um ponto num "n-espaço" com energia

${\displaystyle E_{\vec {n}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}|{\vec {n}}|^{2}\,}$.

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O número de estados com energia menor que E_f é igual ao número de estados que residem em uma esfera de raio ${\displaystyle |{\vec {n}}_{f}|}$ na região do "n-espaço" onde n_x, n_y, n_z são positivos. No estado básico este número iguala o número de férmions no sistema.

${\displaystyle N=2\times {\frac {1}{8}}\times {\frac {4}{3}}\pi n_{f}^{3}\,}$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Os três férmions que ocupam os mais baixos estados de energia formam uma esfera em espaço de momento. A superfície desta esfera é a superfície de Fermi.

o fator é de dois é novamente porque são doisestados de spin, o fator de 1/8 é porque somente 1/8 da esfera repousa na região onde todos n são positivos.

Nós obtemos

${\displaystyle n_{f}=\left({\frac {3N}{\pi }}\right)^{1/3}}$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

então a energia de Fermi é dada por

${\displaystyle E_{f}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n_{f}^{2}}$

${\displaystyle ={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{2/3}}$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Tais resultados em uma relação entre a energia de Fermi e o número de partículas por volume (quando nós substituímos L² com V^2/3):

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m}}\left({\frac {3\pi ^{2}N}{V}}\right)^{2/3}\,}$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A energia de Fermi total de um esfera de fermi de ${\displaystyle N_{0}}$ férmions é dada por

${\displaystyle E_{t}={\int _{0}}^{N_{0}}E_{f}(N)dN={3 \over 5}N_{0}E_{f}}$

${\displaystyle E_{t}={\int _{0}}^{N_{0}}E_{f}(N)dN={\int _{0}}^{N_{0}}{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{\frac {2}{3}}dN}$

${\displaystyle ={\frac {3^{\frac {2}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{2mL^{2}}}{\int _{0}}^{N_{0}}N^{\frac {2}{3}}dN={\frac {3^{\frac {2}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{2mL^{2}}}\left({\frac {3}{5}}N_{0}^{\frac {5}{3}}\right)={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Energia de Fermi total:

${\displaystyle E_{t}={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Integração por substituição:

${\displaystyle E_{t}={\frac {3}{5}}N_{0}E_{f}={\frac {3}{5}}N_{0}\left[{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N_{0}}{\pi }}\right)^{2/3}\right]={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$

${\displaystyle E_{t}={\frac {3}{5}}N_{0}E_{f}}$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

A eliminação de ${\displaystyle L}$ em favor de ${\displaystyle V}$:

${\displaystyle L^{2}=V^{\frac {2}{3}}}$

${\displaystyle E_{t}={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}N_{0}^{\frac {5}{3}}}{10mV_{0}^{\frac {2}{3}}}}}$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Energias de Fermi típicas

Anãs brancas

Estrelas conhecidas como anãs brancas tem massa comparável a nosso Sol, mas têm um raio aproximadamente 100 vezes menor. As alta densidades implicam que os elétrons estão não mais ligados a um núcleo isolado e formam um gás de elétrons degenerado. Os números da densidade de elétrons em uma anã branca são da ordem de 10³⁶ elétrons/m³. Isto significa que sua energia de Fermi é:

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m_{e}}}\left({\frac {3\pi ^{2}(10^{36})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 3\times 10^{5}\ \mathrm {eV} \,}$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Núcleos

Outro exemplo típico é as partículas em um núcleo de um átomo. Os núcleons de um núcleo atômico pode ser tratado, assim, como um gás de Fermi e como tal, modelado.^[2]

O raio do núcleo é aproximadamente^[3]:

${\displaystyle R=\left(1.25\times 10^{-15}\mathrm {m} \right)\times A^{1/3}}$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

onde A é o número de núcleons.

O número densidade de núcleons em um núcleo é conseqüentemente:

${\displaystyle n={\frac {A}{{\begin{matrix}{\frac {4}{3}}\end{matrix}}\pi R^{3}}}\approx 1.2\times 10^{44}\ \mathrm {m} ^{-3}}$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

Agora, como a energia de fermi somente aplica-se a férmions de mesmo tipo, deve-se dividir esta energia por dois. Isto por causa da presença de nêutrons que não afetam a energia de Fermi dos prótons no núcleo, e vice versa.^[4][5][6]

Assim a energia de fermi de um núcleo é dada por:

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m_{p}}}\left({\frac {3\pi ^{2}(6\times 10^{43})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 30\times 10^{6}\ \mathrm {eV} =30\ \mathrm {MeV} }$

///////////////

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

O raio do núcleo admite desvios em torno do valor mencionado acima, então um típico valor para a energia de Fermi normalmente dada é 38 MeV.